Forma dello spazio-tempo
E’ necessario osservare le esplosioni di tipo 1A curando di scegliere solo quelle che sono a
distanza costante da noi nella volta celeste (ad esempio ad un miliardo di anni luce da noi).
Una volta scelte le supernove 1A e stimata la distanza si passa alla misurazione del loro
Redshift e tabulare la loro velocità di espansione calcolabile dall’Effetto Doppler per la luce.
Non mi aspetterei di rilevare le stesse velocità di recessione. Mi aspetterei, invece, piccole
variazioni di velocità alle medesime distanze in punti diversi del cielo. Quindi da un lato
misuro la distanza dall’altra misuro la recessione cioè l’allontanamento dalla nostra
posizione.
Perché la velocità di allontanamento? perché fornisce informazioni sulla topologia
dell’involucro del nostro Universo la cui superficie in espansione è il nostro spazio
quadridimensionale.
Già Einstein aveva descritto, nella Relatività Generale, che la gravità non è una forza. I corpi
sono costretti a muoversi, in uno spazio curvo, secondo la linea più breve che unisce due
punti, infinitesimi, nella loro traiettoria. Credo che questa definizione possa descrivere la
Gravità nel modo più generalizzato possibile.
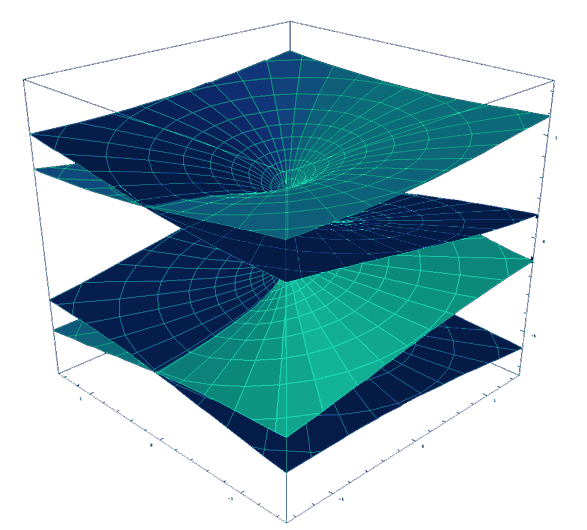
Questa generalizzazione sarà importante per poter giungere alle conclusioni del mio ragionamento. Visto che la gravità è una realtà geometrica sarebbe logico aspettarsi che vi siano altri tipi di curvature che io chiamo “convesse” e cioè opposte a quella creata dai corpi massicci che chiamo “concave”. Sarebbe come far rotolare dei corpi da una collina. Essi si allontanerebbero l’uno dall’altra invece che attrarsi. Il mio parere è che lo spazio-tempo, localmente, può essere “concavo” così come accade tra le stelle massicce, che attirano altri corpi celesti, oppure potrebbe essere “convesso” che porta all’allontanamento di un oggetto dall’altro. Da questa logica di plasticità dello spazio-tempo discende che a seconda della curvatura assunta dallo spazio-tempo esso può addensare le masse, avvicinandole, oppure potrebbe diradarle facendole allontanare. E’ come dire che la gravità possa essere attrattiva o repulsiva a seconda della topologia della porzione di Universo considerata.
Perché ho descritto il concetto di “concavo” e “convesso” ? Perché l’Universo sebbene molto
simmetrico, su vasta scala, possiede delle piccole imperfezioni nella temperatura della
radiazione cosmica di fondo (è un dato di fatto) di circa una parte su 10
5
. Dopo miliardi di
anni queste piccole variazioni di energia, grazie al principio di equivalenza tra massa ed
energia \((E=mc^2)\) hanno cambiato, localmente, e leggermente la velocità con la quale
l’Universo si espande rispetto al valore medio stabilito oggi. Globalmente l’Universo ha
curvatura “convessa” ma, queste piccole variazioni produrrebbero dei cambiamenti nella
curvatura causando degli stiramenti in varie zone dello spazio tempo. Questi stiramenti
produrrebbero un cambiamento, più o meno accentuato, da curvatura convessa a curvatura
concava. Esse sarebbero più o meno accentuate con concavità differenti a seconda del
punto considerato grazie al quantitativo di energia/temperatura posseduto da quel luogo
grazie alle piccole asimmetrie generate durante il Big Bang.
L’effetto globale sarebbe visibile come una spugnosità durante la condensazione della
materia facendoci osservare filamenti di galassie tra enormi spazi vuoti. La materia si è
addensata dove la curvatura è favorevolmente concava e quasi assente dove la curvatura,
invece, è convessa. Come rilevare quindi queste variazioni ?
Dobbiamo rilevare il Redshift della supernova 1A come indicatore di curvatura. Più è elevato il Redshift più velocemente si espanderà quella porzione di spazio-tempo e quindi più accentuata sarà la curvatura convessa dello spazio-tempo. Intorno a questa deformazione la gravità sarà repulsiva. Invece più lento sarà il Redshift più concava sarà quella zona di Universo generando così gravità attrattiva.

Per concludere. La misurazione della velocità di allontanamento, a distanza costante,
sarebbe equivalente a fare la TAC dell’involucro quadridimensionale dell’Universo.
Ripetendo le misure a distanze man mano più elevate (più lontane nel tempo) potremmo
stimare la forma che avevano le varie porzioni di Universo. Utilizzando la quaterna \((x, y ,z, R) \)
dove \(R\) rappresenta il valore di Redshift e \(x,y,z\) la nostra posizione rispetto a tutto il resto)
avremo i dati per stimare la curvatura. Queste varietà di deformazioni non produrrebbero
pozzi gravitazionali veri e propri ma, zone a deformazione più allargata dove la materia
avrebbe potuto condensare più facilmente creando le galassie. Tali deformazioni non così
accentuate avrebbero permesso la nascita di intere galassie. In quelle condizioni la gravità
non seguirebbe la legge dell’inverso del quadrato delle distanze permettendo alle stelle di
ruotare attorno ad esse a velocità costanti come se fossero un tutt’uno così come osservato.
La debole concavità sarebbe responsabile di tutto questo senza per forza tirare in ballo il
concetto di ipotetica Materia Oscura. Gli ammassi di galassie si distribuirebbero sul confine
tra la deformazione concava e convessa nel resto dello spazio-tempo. Nelle porzioni di
universo ove la curvatura sia convessa non potrebbe condensarsi materia generando così
gli enormi spazi vuoti che osserviamo (sebbene la luce verrebbe comunque deviata a causa
della curvatura). Ai confini delle zone convesse dovremmo rilevare zone concave dove la
materia ha potuto condensarsi in filamenti di galassie. Infine scendendo sempre più nel
particolare all’interno della zona concava, nelle galassie, la massa deformerebbe ancor di
più la curvatura rendendola ancora più convessa in modo tale da generare stelle e pianeti
rispettando la legge dell’inverso del quadrato delle distanze. In definitiva la visione che
avremmo sarebbe quello di uno spazio-tempo grumoso come una spugna.
Questo ragionamento, se verificato dalle osservazioni descritte, sarebbe una alternativa più
accettabile, più convincente rispetto al concetto della ipotetica Materia Oscura.
Spero di essere riuscito a spiegarmi a sufficienza ma, sono disponibile per ulteriori
approfondimenti.
Antonello Di Gioia