I terribili tensori
\(R_{\mu\nu}\) è un tensore, cosiddetto “di Ricci” perché il calcolo su questi oggetti, è stato inventato o “scoperto” da Gregorio Ricci Curbastro, un matematico italiano nativo di Lugo nella provincia di Ravenna. Cosa sono questi tensori?
Un tensore è un oggetto che racchiude una caratteristica cruciale per i fisici:
"un tensore è sempre lo stesso in ogni sistema di riferimento!"
Questo fatto, spesso, sicuramente l’avrete sentito dire da qualche parte, si dice in gergo dei fisici che un tensore trasforma in modo covariante. Praticamente il tensore è una raccolta di oggetti – (numeri, funzioni… operatori) che soddisfano a delle proprietà speciali. Ecco come si presenta in generale 😎:
$$ \overline{T_{j_1\ldots j_n}^{i_1\ldots i_m}} = T_{p_1\ldots p_\xi}^{q_1\ldots q_\eta} {\partial \overline{x}^{j_1}\over \partial x^{p_1}}\ldots {\partial \overline{x}^{j_n}\over \partial x^{p_\xi}}{\partial x^{q_1}\over \partial \overline{x}^{i_1}}\ldots {\partial x^{q_\eta}\over \partial \overline{x}^{i_m}}$$
La cosa fondamentale da capire però è che mentre il tensore in sé è invariante, la sua rappresentazione, cioè tutte le sue componenti si trasformano in modo tale da mantenerlo covariante! Tutto quì. L’equazione di sopra serve a questo, ci sono una serie di derivate parziali, che in realtà sono matrici jacobiane di tipo bacward o forward, cioè trasformazioni dirette o inverse, ma è solo una questione tecnica.
Questo è un generico campo tensoriale di tipo \(n, m\) nel senso che ha \(n\) indici alti (controvarianti\) ed \(m\) indici bassi covarianti, di nuovo i termini “controvariante” e “covariante” sono legati alle tipologie di trasformazioni delle componenti del tensore.
Ora, un matematico potrebbe dire naturalmente che la definizione di tensore è qualcosa di più simile a “una mappa multilineare da vettori e vettori duali a numeri reali”, ma per adesso lavoriamo con l’approcio da fisici…
Il tensore di Ricci ha due indici covarianti, la sua legge di trasformazione diventa semplicemente:
$$ \overline{R_{\mu\nu}} = R_{ij}{\partial x^{i}\over \partial\overline{x}^\mu}{\partial x^{j}\over \partial\overline{x}^\nu} $$
Ha rango \(2\) e quindi intrinsecamente è bidimensionale, possiamo raggruppare tutet le sue componenti \(R_{\mu\nu}\) in una matrice quadrata, che attenzione non è detta che per forza sia \(2\times 2\), questo dipende dallo spazio in cui risiede, ad esempio nella relatività, è una matrice \(4\times 4\) come questa:
$$ R_{\mu\nu} = \begin{pmatrix} R_{00} & R_{01} & R_{02} & R_{03} \\ R_{10} & R_{11} & R_{12} & R_{13} \\ R_{20} & R_{21} & R_{22} & R_{23} \\ R_{30} & R_{31} & R_{32} & R_{33} \end{pmatrix} $$
Ora basta parlare di tecnicismi… se vuoi rempirti il cervello di queste bellezze, puoi seguire la mia piccola guida Easy sull’analisi tensoriale qui
La Geometria Ricciana
Cosa vuol dire geometricamente il Tensore di Ricci? I fisici vogliono vedere le cose, immaginarsele come faceva Einstein mentre era a Berna all’ufficio brevetti, o lungo i giardini a Princeton durante le sue passeggiate immerso nella natura…
Il Tensore di Ricci si ottiene da un altro tensore più grande e generico, “Il Tensore di Riemann” che racchiude tutta l’informazione sulla curvatura di uno spazio. La “matematizzazione” di oggetti come le superfici o le brane o gli spazi curvi, avviene in quello che i matematici chiamano varietà. Tutta questa informazione spesso non ci serve è quindi il tensore di Riemann viene strizzato come una spugna da contrazioni e semplificazioni, et voilà ecco spuntare il Tensore di Ricci.
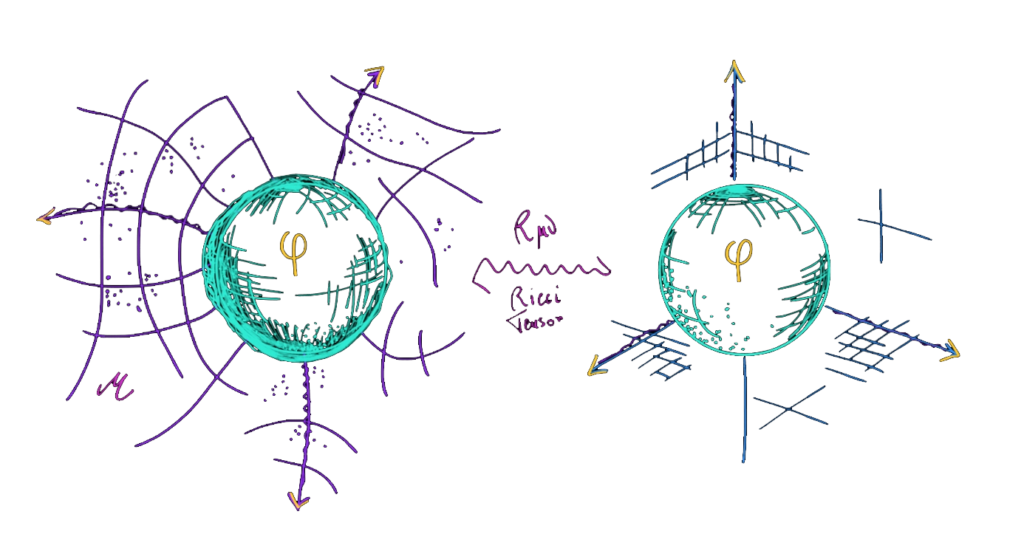
L’interpretazione geometrica del Tensore di Ricci è molto semplice:
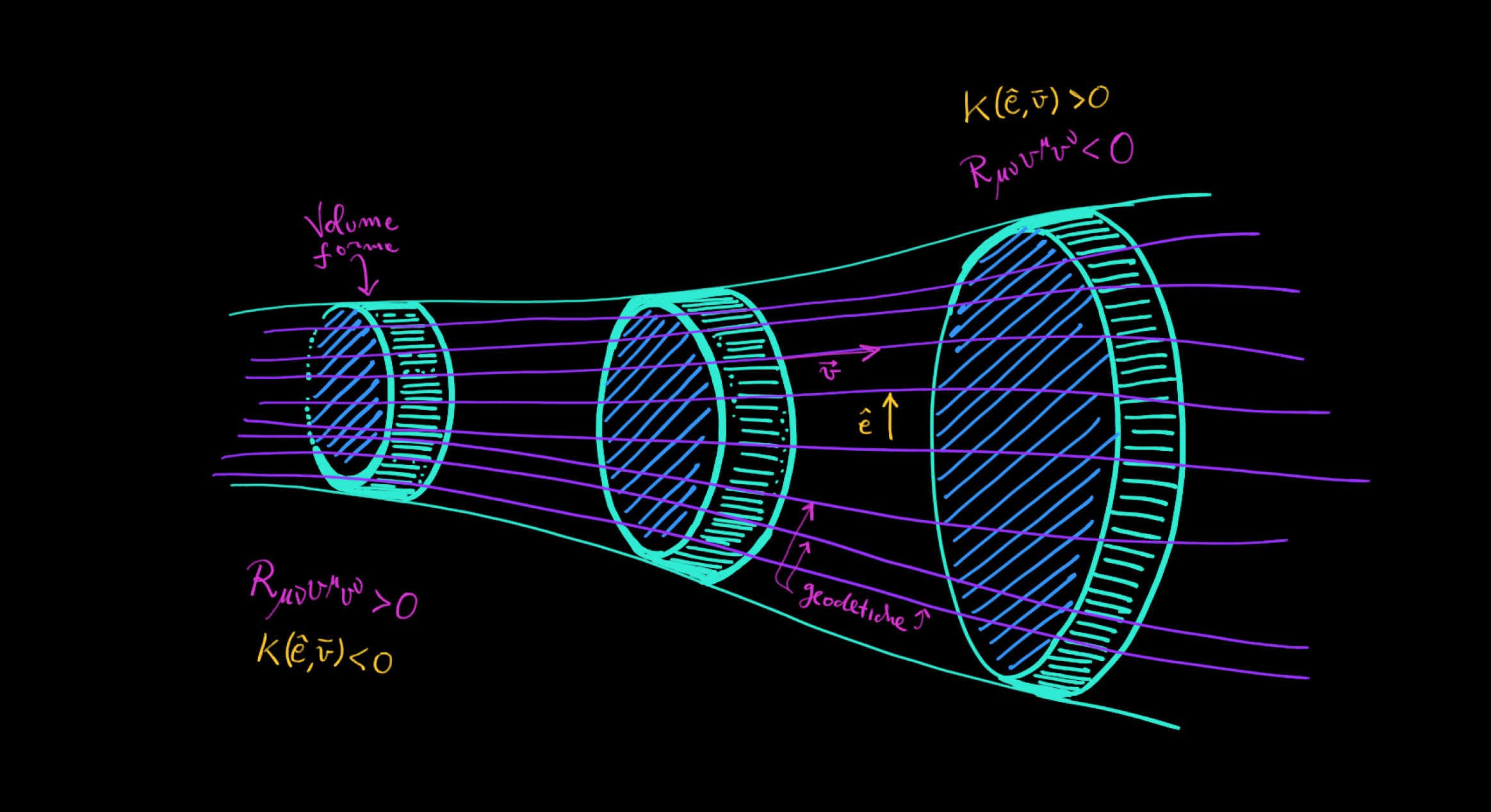
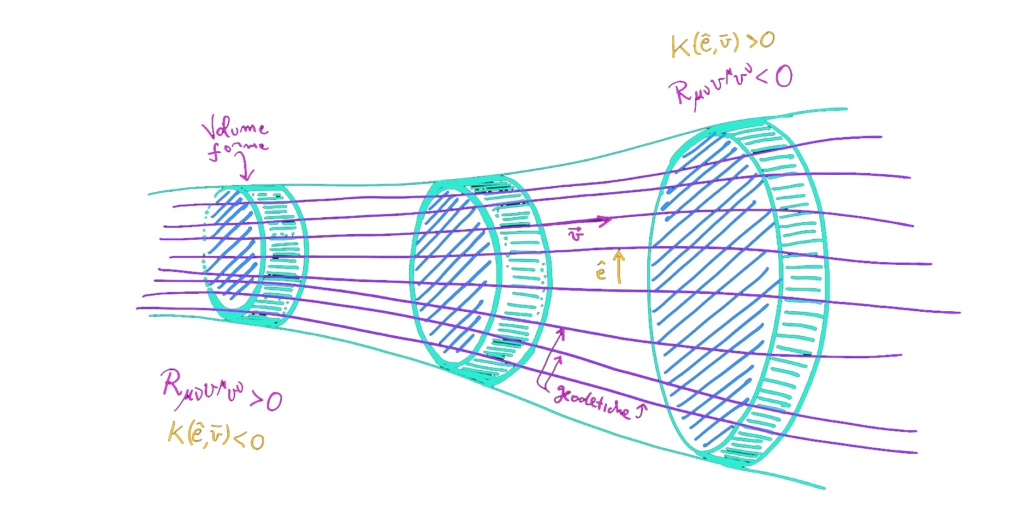
Esso descrive la differenza che c’è tra una sfera nello spazio euclideo ed una in uno spazio curvo. In sostanza misura come cambia il volume quando muovo la sfera da uno spazio all’altro. Questo succede perché le geodetiche cambiano per via della curvatura, ed il tensore di Ricci ci restituisce proprio questa variazione.
Per spazio curvo mi riferisco essenzialmente a una varietà riemanniana, che per dirla semplicemente è semplicemente uno spazio in cui i vettori di base possono variare da luogo a luogo (e la geometria di quello spazio è descritta da un tensore metrico). Ecco comparire un altro tensore… ma quanti ce n’è sono direte….
In RG questo si traduce nel descrivere come cambia il volume dello spaziotempo a causa di maree gravitazionali e variazioni del campo gravitazionale in presenza di masse.
Algebra, carte locali e Simboli di Christoffel
Capito essenzialmente cosa fa il Tensore di Ricci, molti si chiederanno come è fatto e come si calcola praticamente? Per rispondere a questa domanda bisogna analizzare alcune delle sue proprietà e vedere localmente: (metaforicamente parlando, con un microscopio) come appare:
Prendiamo il tensore di Riemann:
$$ R^i_{jkm} = {\partial \Gamma^i_{jm} \over \partial x^k} – {\partial \Gamma^i_{jk} \over \partial x^m} + \Gamma^i_{rk}\Gamma^r_{jm} – \Gamma^i_{rm}\Gamma^r_{jk} $$
Se facciamo una contrazione del primo e del terzo indice: \( i \equiv k\) contrazione vuol dire praticamente che si eguagliano i due indici e si applica la convenzione di Einstein in cui si sommano i termini con gli indici ripetuti da \(1\) ad \(n\).
Simmetrie e torsioni
Una delle caratteristiche principali del tensore di Ricci, che derivano dal suo genitore, il Tensore di Riemann sono le simmetrie, la più importante delle quali è la seguente:
$$ R_{ij} = R_{ji} $$
Capita spesso che uso indici diversi, \(\mu\) e \(\nu\) si usano in relatività, \(i\) e \(j\) più in generale.
Questa simmetria deriva a sua volta da una proprietà più intrinseca dello spazio riemanniano (e quindi anche nella RG) ossia la torsione!
L’esempio più semplice di torsione è quello che si ottiene con un filo. Basta ruotarlo con le dita ed esso si torce. Potete appiccicare un foglietto o un nastro sul filo per vederla in azione.
Nella geometria riemanniana questo concetto primordiale è descritto da un altro tensore chiamato Tensore di Torsione \( T^i_{jk}\), definito nel modo seguente:
$$ T^i_{jk} = \Gamma^i_{jk} – \Gamma^i_{kj} $$
Questo tensore, valuta la differenza tra due simboli di Christoffel con gli indici bassi scambiati, se questa differenza è nulla, la torsione è nulla e lo spazio risulta particolarmente simmetrico
Esempi
Vediamo finalmente, come si calcola il tensore di Ricci di uno spazio riemanniano. I passaggi per determinarlo sono i seguenti:
- Calcolo del Tensore metrico \(g_{ij}\).
- Calcolo dei Simboli di Christoffel \(\Gamma^i_{jk}\).
- Calcolo del Tensore di Ricci \(R_{ij}\)
Ora, di questi tre punti, il grosso del lavoro sono i primo due. Una volta che si hanno a disposizione i simboli di Christoffel ed il tensore metrico, il passaggio al Tensore di Ricci è pressoché immediato.

Spazio Piatto
Il tensore di Ricci in uno spazio piatto è 0.
$$ R_{ij} = 0 $$
Banalmente si tratta dell’esempio più semplice di tutti, ma nasconde un’insidia. Se lo spazio è piatto sicuramente \(R_{ij} = 0\) ma non vale il contrario. Questo perché il Tensore di Ricci non possiede tutta l’informazione sulla curvatura, cosa che invece è contenta del Tensore di Riemann.
Sfera
Il caso della sfera è un classico, per la sua simmetria intrinseca. Stiamo parlando di una 2-Sfera, quindi non studiamo la sfera dal punto di vista di \(R^3\) ma direttamente dalla sua geometria locale.
In questo caso, è facile intuirlo perché il suo tensore metrico sarà una matrice \(2\times 2\). Partiamo dalla forma differenziale quadratica (elemento di linea):
$$ ds^2 = r^2d\theta^2 + r^2sin^2\theta d\phi $$
Il tensore metrico si ottiene facilmente da essa:
$$ g_{ij} = \begin{pmatrix} r^2 & 0 \\ 0 & r^2sin^2\theta \end{pmatrix} $$
Consideriamo ora la definizione di simbolo di Christoffel:
$$ \Gamma^i_{jk} = {1\over 2}g^{i\lambda}\left( {\partial g_{\lambda j} \over x^k} + {\partial g_{\lambda k} \over x^j} – {\partial g_{jk} \over x^\lambda}\right) $$
E’ facile convincersi che valgono le seguenti relazioni:
$$ \Gamma^1_{11} = \Gamma^1_{12} = \Gamma^1_{21} = \Gamma^2_{11} = \Gamma^2_{22} = 0$$
$$ \Gamma^2_{12} = \Gamma^2_{21} = cot\theta $$
$$ \Gamma^1_{22} = -sin\theta cos\theta $$
Applicando la definizione si ottiene facilmente l’espressione del Tensore di Ricci della 2-Sfera:
$$ R_{ij} = \begin{pmatrix} 1 & 0 \\ 0 & sin^2\theta \end{pmatrix} $$