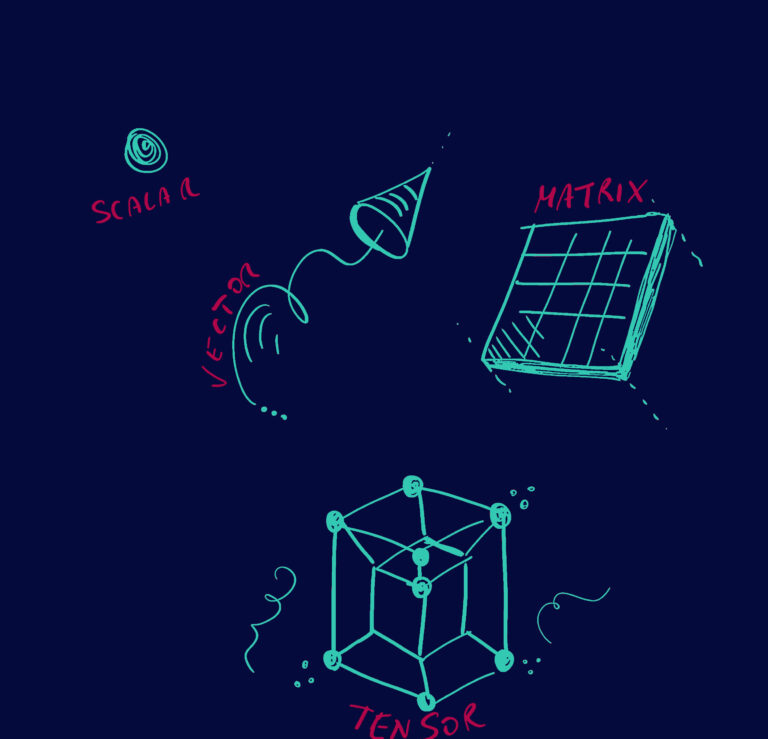
La formula di Taylor
Se c'è uno strumento, che ogni fisico e/o matematico deve assolutamente conoscere,
questo è la Formula di Taylor, che rappresenta il coltellino svizzero, tuttofare,
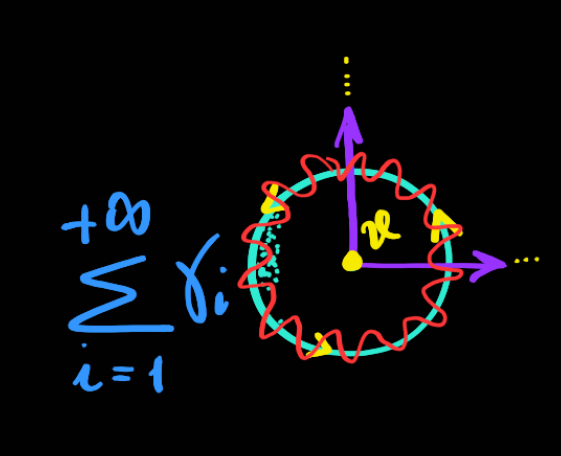
che risolve i problemi ogni qualvolta ci si presenta un mostro di funzione o espressione irrisolvibile per via analitica, ma approssimabile in ogni caso. Prima di iniziare, vi presento la formula e poi la spieghiamo: $$ f(x)_{x_0, k} = \sum_{k=0}^\infty \left( {f^{(k)}(x_0) (x-x_0)^k \over k! } \right) $$