In un’epoca non molto lontana dalla nostra, dove personaggi illustri del calibro di Gauss, Newton ed Einstein (solo per citarne alcuni) grandi cultori e profondi conoscitori della scienza,
capitava spesso, che le scoperte avvenivano per la loro profonda visione d’insieme di cose che apparentemente diverse, costituivano un tutt’uno; famosa è l’unificazione
fra elettricità e magnetismo ad opera di James Clerk Maxwell nel 1865.
Oggi è raro trovare queste figure perché siamo specializzati in settori specifici, ma quando diverse aree scientifiche apparentemente diverse si uniscono, nascono dei connubi indissolubili, che solo grandi menti riescono ad afferrare.
La cosiddetta computazione quantistica, di cui tratteremo alcune idee in questo articolo è una disciplina che nasce negli anni 80 come una
commistione di idee tratte sia dalla meccanica quantistica che dall’informatica.
Tra le mille cose che questi dispositivi elettronici sanno fare con straordinaria velocità e precisione, c’è, fortunatamente, una cosa che essi non sanno fare e risultano, pertanto, assai inefficienti;
si tratta dei contesti legati alla creatività ed alle emozioni, correlati all’emisfero destro del nostro cervello, quindi al pensiero che va al di là della logica.
Se hai capito la meccanica quantistica, allora significa che non l’hai capita
Niels Bohr
Il computer quantistico
Un computer quantistico è un dispositivo elettronico, che, rispetto all’approccio tradizionale basato sulle porte logiche irreversibili e sui flip-flops si
fonda sulle leggi della meccanica quantistica come ad esempio l’entanglement e la sovrapposizione degli effetti.
Con buona probabilità esso è in grado di svolgere “più soluzioni per un singolo problema nello stesso momento” piuttosto che svolgere calcoli sequenziali. Il tutto a una velocità senza precedenti.
Ma quali sono le caratteristiche concettuali e su cosa si fonda un computer quantistico? Diamo una visione d’insieme.
$$ \diamond\diamond\diamond $$
Caratteristiche rispetto al modello classico: l’alba di una nuova era
In un computer tradizionale, che ritroviamo sulle nostre scrivanie, in uno smartphone piuttosto che in un televisore o in un qualunque circuito logico digitale irreversibile, l’informazione è rappresentata sotto forma di bit, i quali
possono assumere solo due stati possibili, come ad esempio due facce di una moneta, un valore di verità vero o falso, una lampada accesa o spenta ecc.
In tutti questi esempi gli stati sono mutuamente esclusivi, ossia l’uno implica l’assenza dell’altro. Questi stati concretamente, vengono realizzati a livello circuitale rilevando
il passaggio o il non passaggio di corrente nelle cosiddette porte logiche elementari, che sono a fondamento di tutta l’architettura e la logica dei calcolatori.
Ma il passaggio, ed il riconoscimento di uno stato è possibile, per via del tutto sommaria attraverso lo spostamento di migliaia di particelle (flusso di elettroni). Sostanzialmente, un singolo bit, ciò che noi rappresentiamo con 0 o con 1, ovvero,
l’unità elementare dell’informazione è rappresentata dallo spostamento di un’enorme quantità di particelle.


Nella versione quantistica questi stati si riferiscono, invece al comportamento di singole particelle elementari, es. elettroni, fotoni ecc; è possono trasportare un’unità singola di informazione (0 oppure 1), un notevole incremento delle prestazioni, ma
c’è una novità!, gli stati possono sovrapporsi l’un l’altro in una “logica probabilistica“, – ricorderete il paradosso del gatto di Schrödinger che risulta sia morto che vivo contemporaneamente fintantoché non apriamo la scatola in cui è rinchiuso…,
analogamente, qui gli stati possono valere ambedue, essere, cioè sovrapposti l’un l’altro (termine
più propriamente espresso, come, « entangled » e collassare in uno stato concreto, quando si interagisce con le particelle.
Questi oggetti astratti vengono chiamati qubit (quantum bit) o bit quantistici; e lo scopo di questo articolo è carpire alcune delle loro proprietà fondamentali.
Come detto un bit classico può avere solo due stati \( 0\) o \(1\); analogamente un bit quantistico (qubit) può avere due stati elementari che rappresenteremo con i simboli:
$$ {\huge |0\rangle \hspace{6mm} |1\rangle } $$
$$ {\large |0\rangle = \begin{pmatrix} 1 \ 0 \end{pmatrix}}, \hspace{5mm}{\large |1\rangle = \begin{pmatrix} 0 \ 1 \end{pmatrix}} $$
Stati e vettori
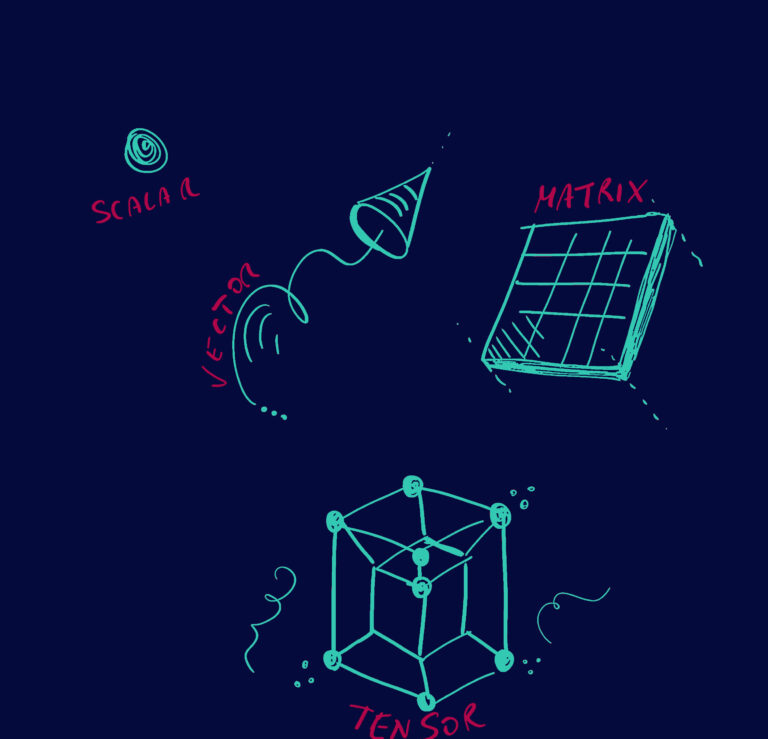
Facciamo ora la seguente osservazione: se nella logica tradizionale questi stati elementari sono rappresentati da numeri “singleton” (singoletti) –
i fisici li chiamerebbero scalari, nella loro versione quantistica essi sono dei vettori complessi espressi secondo la notazione
bra-ket di Dirac (per chi non sapesse cos’è la notazione di Dirac, non c’è problema, possiamo sempre fare riferimento a dei semplici vettori colonna, vi invito,
comunque a dare un’occhiata su wikipedia o su altre fonti).
Senza addentrarci troppo in dettagli tecnici per la legge di sovrapposizione gli stati possono valere entrambi, e questo è possibile attraverso la definizione del vettore di stato \( |\psi\rangle \) espresso
come combinazione lineare dei due vettori di partenza.

$${\Large |\psi\rangle = \alpha|0\rangle + \beta|1\rangle }$$
$${ \alpha\begin{pmatrix} 1 \ 0 \end{pmatrix} +\beta\begin{pmatrix} 0 \ 1 \end{pmatrix} = }$$
$$\LARGE \begin{pmatrix} \alpha \ \beta \end{pmatrix} $$
La possibilità che si verifichi uno dei due eventi associati ai due vettori di stato elementari è espressa
attraverso la legge di probabilità tipica della meccanica quantistica.
$$ {\Large |\alpha|^2 + |\beta|^2 = 1}$$
dove in generale \( |\alpha|^2 = \alpha\cdot \overline{\alpha} \) (prodotto del complesso per il suo coniugato), è la probabilità che si verifichi l’evento associato al vettore di stato \( |0\rangle \), stesso discorso per \( \beta \).
Abbiamo quindi scoperto che l’equivalente della logica booleana, la logica quantistica, è basata su vettori complessi chiamati qubit con delle proprietà simili a quelle delle particelle elementari, cerchiamo ora di capire come
potrebbero essere progettati i circuiti elementari di un computer quantistico.
$$ \diamond\diamond\diamond $$
Logica quantistica
Se un computer tradizionale è costruito su porte logiche a transistor, i qubit viaggiano nelle porte logiche quantistiche, ossia,
porte speciali con capacità che vanno oltre le leggi classiche della fisica, la più semplice delle quali è sicuramente l’inverter NOT o negazione logica.
Un inverter tradizionale effettua un’inversione di segnale: (se l’input è \(1\), l’output sarà \(0\) e viceversa) un elemento essenziale nella realizzazione circuitale
degli elaboratori, il corrispettivo quantistico dell’inverter è l’inverter di stato.
Dal momento che un qualunque qubit \( |\psi\rangle \) è rappresentato dalla combinazione dei vettori di stato l’invertitore deve semplicemente trasformare un vettore
\( |\psi\rangle = \begin{pmatrix} \alpha \ \beta \end{pmatrix} \) in un vettore \( \overline{|\psi\rangle} = \begin{pmatrix} \beta \ \alpha \end{pmatrix} \).
Ora, cos’è che trasforma (matematicamente) un vettore colonna in un altro vettore colonna lasciandone inalterate le dimensioni? Ebbene, chi ha studiato un pò di geometria ed algebra
saprà sicuramente o ricorderà che si tratta di una matrice \( {\mathbb M}\) di trasformazione, e l’operazione è il prodotto di questa matrice \( {\mathbb M}\) per il vettore di stato \(|\psi\rangle \).
$${\large {\mathbb M}|\psi\rangle = \overline{|\psi\rangle} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} }$$
Matrici
Sorprendentemente, l’analogo delle semplici operazioni elementari dell’algebra booleana tradizionale è sostituito da matrici nella logica-quantistica dei qubits, e la porta NOT
è un caso particolare quando si sceglie come \( {\mathbb M} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \). In generale tuttavia una porta-quantistica ad un singolo qubit è
rappresentata dalla trasformazione unitaria sui bits di stato.
$${\large \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \alpha \ \beta \end{pmatrix} = \begin{pmatrix}a\alpha + b\beta \\ c\alpha + d\beta \end{pmatrix}}$$
Questa matrice soddisfa a delle regole speciali come la legge di probabilità e l’unitarietà, ma non è l’unica. Vediamo di cosa si tratta più in dettaglio. Per capirlo bisogna aver ben chiaro
il concetto di matrice trasposta e coniugata. Sono dei concetti semplici ma che è bene ribadire per rinfrecare le idee al lettore. Anzitutto una matrice è una tabella fatta di righe e colonne
contenente di solito numeri (ma anche oggetti più complessi), ora una trasposta si ottiene semplicemente scambiando le righe con le colonne della matrice di partenza, e la coniugata è la matrice dei complessi coniugati, dal momento
che gli elementi della matrice, specialmente in ambito quantistico sono dei numeri complessi.
Ebbene, se una matrice \( {\mathbb M} \) è tale per cui la sua trasposta-coniugata, che indicheremo con \( {\mathbb M^{\dagger}}\) soddisfa la segunete relazione: $$ {\Large {\mathbb M^{\dagger}}{\mathbb M} = {\mathbb I}} $$ Essa si dice unitaria.
La matrice \( {\mathbb M} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \) è certamente unitaria; infatti:
$$ {\mathbb M} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} $$
$$ \downarrow $$
$$\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = {\mathbb I} $$
Ma non è la sola, esistono altre matrici con questa caratteristica, che suggeriscono una prima sostanziale differenza con l’approccio classico che vede un singolo inverter non banale per l’inversione dei bit.
La Matrice di Hadamard
La matrice \({\mathbb H}\) di Hadamard è anch’essa unitaria; la sua definizione è:
$$ {\large \mathbb H} = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\1 & -1 \end{pmatrix} $$
$$ { \mathbb H^{\dagger}\mathbb H} = \frac{1}{2}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} = $$ $$ = \frac{1}{2}\begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} $$
Osservate come la matrice di Hadamard coincide con la sua matrice aggiunta
$${ \mathbb H^{\dagger} = \mathbb H} $$
In questo caso si dice che essa è auto-aggiunta.
Tutti gli operatori elementari, vengono sostituiti da matrici di trasformazione e gli stati vengono trasformati mediante una semplice operazione di prodotto. Naturalmente è possibile
progettare porte a 2, 3 o più qubits, l’idea rimane la stessa, cambia il numero di componenti nei vettori ed il numero di combinazioni e di stati rappresentabili con un singolo qubit.
$$ \diamond\diamond\diamond $$
Fantascienza o realtà? Back to the future
Se da un punto di vista teorico, un computer quantistico è un insieme di teorie matematiche fondate su leggi fisiche ben solide, praticamente la sua realizzazione
risulta alquanto complessa per un semplice fatto noto come decoerenza quantistica, che rappresenta l’inevitabile interazione tra il sistema quantistico e l’ambiente in cui esso è immerso,
ed è conseguenza del Principio di indeterminazione di Heisemberg; del resto costruire una porta quantistica ad esempio a fotoni
richiederebbe un apparato ottico fatto di specchi riflettori, fotodiodi, interferometri, collimatori –
che causerebbero, durante il loro funzionamento, errori nelle misure e perturbazioni annullando le sovrapposizioni (ricordate che quando aprite la scatola il gatto di Schrödinger o è vivo o è morto ma non entrambi, avete collassato un evento)
quando misuriamo un fascio di fotoni infatti secondo Heisemberg la misura è affetta da errori dovuti agli strumenti stessi i quali disturbano l’andamento del campo elettromagnetico
al diminuire della lunghezza d’onda con cui lo osserviamo.



Ma le sorprese non finiscono quì, un gruppo di fisici, stà lavorando ad un progetto che vede la possibilità di “fondere” un computer quantistico con una macchina del tempo. S. Aaronson dice:
«di fronte ad una macchina del tempo i quantum computer apparirebbero inutili come i distributori di bevande» , si potrebbe addirittura far uso dei vecchi computer a valvole del dopoguerra dal momento che con delle macchine del tempo si possono superare quasi tutti limiti
imposti dalla fisica, ed impiegare tutto il tempo che si vuole e solo tipo aver terminato la computazione trasmettere il risultato dal passato
al presente; tuttavia sono l’oggetto più complesso che si possa mai realizzare.
Il futuro
Possiamo in conclusione affermare di essere ancora molto lontani da un prototipo funzionante di computer quntistico perfetto, tuttavia molti colossi dell’informatica come Google, Intel e IBM stano investendo cospicue
somme in questa direzione e sono giunti alla realizzazione di veri e propri simulatori cloud quantistici, e processori a qubit -Intel ha già sfornato il suo primo processore a 17qubit ed IBM ha promesso che nel 2018 renderà disponibile il suo nuovo processore IBM-Q a 50qubit
oltre ad un sistema cloud online con accesso al simulatore quantistico.
Questa potrebbe essere la svolta alla possibilità di costruire supercalcolatori dalle prestazioni estreme in grado di simulare il ragionamento di un cervello umano, cosa alquanto improbabile ai giorni nostri
dove i supercomputer vincono qualche partita a scacchi o cercano inesorabilmente di superare la barriera dell’A.I. con il Test di Turing… Potremmo continuare a discuterne appassionatamente ma credo che ci sarà occasione futura, per adesso è tutto
io sono quì, anzi, noi siamo quì, ansiosi, nell’attesa di una nuova era.