I numeri complessi, rappresentano una estensione dell’insieme \( \mathbb R\) dei numeri reali. I motivi di questa estensione sono molteplici. Come primo esempio ricordo l’impossibilità di risoluzione delle equazioni di secondo grado, quando il discriminante è negativo – se ci restringiamo ai soli numeri, reali… ma del resto i matematici amano fantasticare con la mente, e come al solito si inventano delle bellissime strutture algebriche astratte, che per gioco forza poi entrano a far parte del mondo della fisica e si permeano nei modi più assoluti e straordinari, nella descrizione dei fenomeni naturali.
$$ \diamond $$
Definizione
Un numero complesso è rappresentato da un’espressione del tipo: \( z = x+iy \), dove \( x \in \mathbb R\) ed \( y \in \mathbb R \), sono per l’appunto numeri reali nel senso a noi noto. Più propriamente, la \( x\) si chiama parte reale del numero complesso e la si indica come ( Re(z)), mentre la ( y) si chiama coefficiente dell’immaginario o (parte immaginaria) e la si indica come \( Im(z)\). Ovviamente, ripeto abbiamo che:
$$ z= x+iy, \hspace{4mm} \begin{cases} x = Re(z) \in \mathbb R \ y = Im(z) \in \mathbb R \end{cases} \} $$
L’insieme dei numeri complessi lo indichiamo con la lettera ( \mathbb C ). La definizione dell’insieme \( \mathbb C\) è data dalla seguente espressione insiemistica:
$${\large \mathbb C = \left\{ z = x+iy: x\in \mathbb R, y \in \mathbb R, i^2 = -1\right\} }$$
Per gli insiemi numerici studiati fin dalle scuole medie inferiori, valgono le seguenti inclusioni insiemistiche:
$$ {\large \mathbb N \subseteq \mathbb Z \subseteq \mathbb Q \subseteq \mathbb R \subseteq \mathbb C } $$
$$ \diamond $$
Operazioni elementari
Su questo insieme numerico, valgono le usuali operazioni elementari di somma +, differenza –, moltiplicazione \( \cdot\) e quoziente / definite nel modo seguente. Non vale invece, l’ordinamento
naturale dei numeri complessi, rispetto ai numeri reali, che godono di un ordinamento standard.
Consideriamo due numeri complessi \( z_1 = x_1+\color{#008080}{i}y_1 \) e \( z_2 = x_2+\color{#008080}{i}y_2 \)
allora valgono le seguenti operazioni elementari
$$ z_1 + z_2 = (x_1+\color{#008080}{i}y_1) + (x_2+\color{#008080}{i}y_2) = (x_1+x_2)+\color{#008080}{i}(y_1+y_2) $$
$$ z_1 – z_2 = (x_1+\color{#008080}{i}y_1) – (x_2+\color{#008080}{i}y_2) = (x_1-x_2)+\color{#008080}{i}(y_1-y_2) $$
$$ z_1z_2 = (x_1+\color{#008080}{i}y_1)(x_2+\color{#008080}{i}y_2) = (x_1x_2-y_1y_2)+\color{#008080}{i}(x_1y_2+y_1x_2) $$
$$ {z_1 \over z_2} = z_1z_2^{-1} = {(x_1+\color{#008080}{i}y_1) \over (x_2+\color{#008080}{i}y_2) } =
\Biggl( {x_1x_2+y_1y_2 \over x_1^2 + x_2^2} \Biggr) +
\color{#008080}{i}\Biggl( {y_1x_2-x_1y_2 \over x_1^2 + x_2^2} \Biggr) $$
$$ \diamond $$
Coniugato
Per ogni numero complesso \( z = x+\color{#008080}{i}y\) è definito il complesso coniugato, indicato con \( \overline{z}\) o \( z^*\) tale per cui si ha: \( \overline{z} = x-\color{#008080}{i}y\).
$$ Re(z) = Re(\overline{z}) \hspace{5mm} Im(z) = -Im(\overline{z}) $$
Inoltre valgono le seguenti relazioni che mettono in relazione le parti reali ed immaginarie con il coniugato:
$$ Re(z) = {z + \overline{z} \over 2} \hspace{5mm} Im(z) = {z – \overline{z} \over 2\color{#008080}{i}} $$
$${ z = {z + \overline{z} \over 2} + \color{#008080}{i}{z – \overline{z} \over 2\color{#008080}{i}} }$$
Risulta facile verificare che vale la seguente relazione molto importante:
$$ {\Large z \overline{z} = |z|^2} $$
Dove \( |z| \) è un numero puramente reale ed è il modulo del numero complesso \( z\).
Esprimendo il numero \( z\) nella sua parte reale ed immaginaria (lo stesso per il coniugato), abbiamo:
$$ (x+\color{#008080}{i}y)(x-\color{#008080}{i}y) = (x^2+y^2) +
\color{#008080}{i}(xy-xy) = (x^2+y^2) = |z|^2 \hspace{2mm}_\square $$
Avendo introdotto il coniugato di un numero complesso ed il modulo, il quoziente di due numeri complessi assume la forma seguente più compatta:
$$ {\large {z_1 \over z_2} = {z_1\overline{z_2} \over z_2\overline{z_2}} = {z_i\overline{z_2} \over |z_2|^2 } }$$
$$ \diamond $$
Geometria dei numeri complessi
La prima volta che apparvero, i numeri complessi, suscitarono scalpore tra i matematici del ‘500. non è un caso che il nome “immaginari“, si riferisse
al fatto che questi oggetti erano delle quantità astratte distanti dal concetto classico di numero inteso come pura espressione della quantità. per molto tempo, questi enti furono impiegati
senza avere una conoscenza diretta, solo per il semplice fatto che essi “funzionavano”. Fino a quando i matematici Wessel, Argand e Gauss arrivarono indipendentemente
ad una interpretazione geometrica, semplice ed elegante, per questo, potente ed efficace che
finalmente porto alla piena comprensione ed accettazione dei numeri complessi
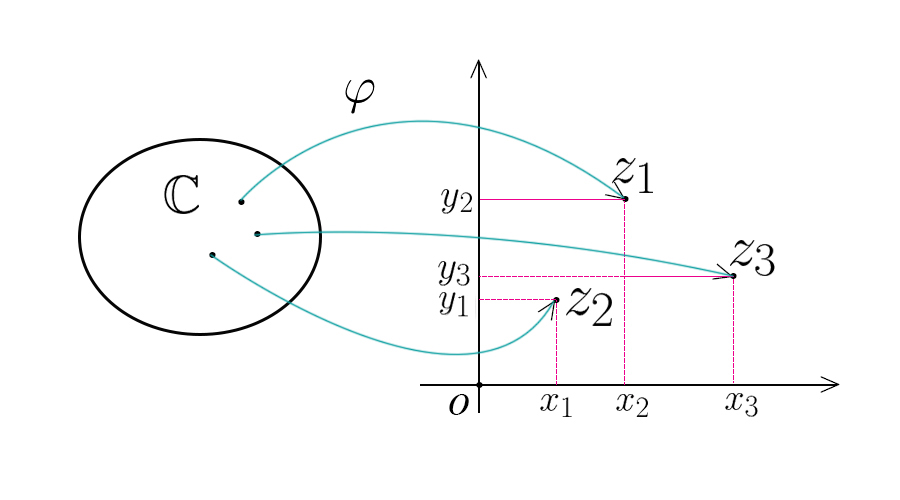
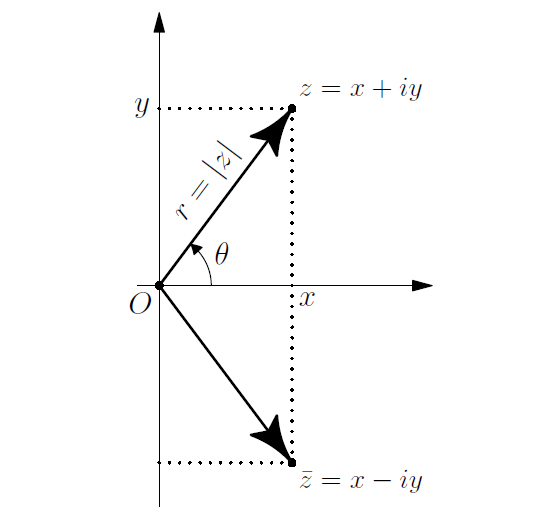
Tale interpretazione consiste, semplicemente, nell’associare, ogni numero complesso \( z = x+\color{#008080}{i}y \) con un punto del piano euclideo \( \mathbb R^2\). In questo modo, la parte reale e la parte immaginaria,
assumono il ruolo di ascissa ed ordinata di un punto \( P(x, y)=(Re(z), Im(z))\) ed il piano è chiamato
piano di Argand-Gauss o più semplicemente: piano complesso.
$$ {\large \varphi: \mathbb C \rightarrow \mathbb R^2} $$
$${\large \mathbb C \ni (x+\color{#008080}{i}y) \longrightarrow \begin{pmatrix} x \ y
\end{pmatrix} \in \mathbb R^2} $$
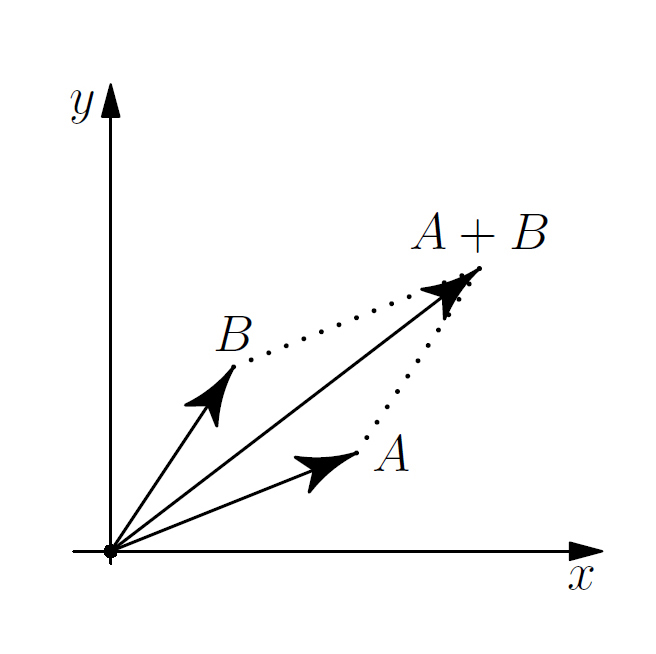
Nel piano complesso, le operazioni assumono una interpretazione grafica molto suggestiva. I numeri complessi, si comportano in modo simile ai vettori bidimensionali, ad esempio
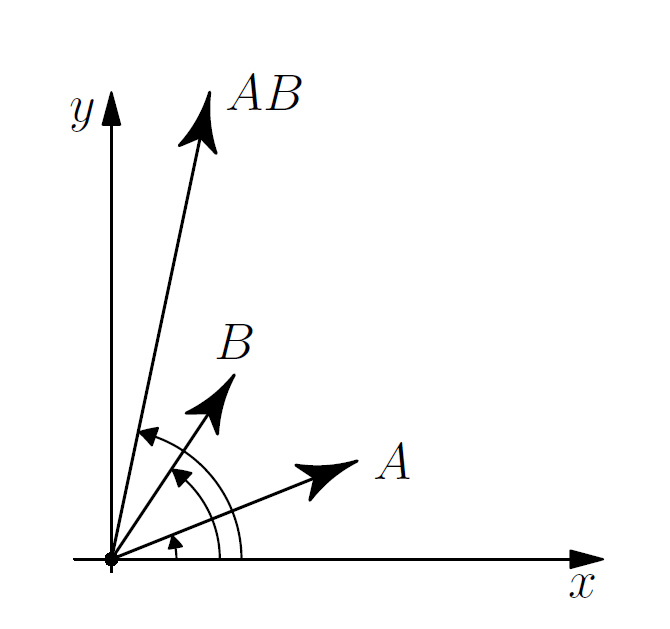
la somma, soddisfa alla famosa regola del parallelogramma, tipica dei corsi di fisica, il coniugato è una semplice simmetria rispetto all’asse reale delle \( x\)… e così via. Interessante è il prodotto
che rappresenta uno stiramento combinato una rotazione nel piano complesso.
$$ \diamond $$
Forma trigonometrica
Ogni numero complesso ( z), abbiamo visto, nel piano complesso si rappresenta come un vettore di \( \mathbb R^2\). Se consideriamo il triangolo rettangolo \( OzE \), formato tra l’origine, il punto origine degli archi
ed il numero complesso \( z\), dalla trigonometria elementare possiamo esprimere \(z\)
nella sua forma trigonometrica
$$ z = \rho cos\theta + \color{#008080}{i}\rho sin\theta = \ \rho( cos\theta + \color{#008080}{i} sin\theta ) $$
$$ \begin{cases} x = \rho cos\theta \ y = \rho sin\theta \end{cases} $$
In questo modo \( \rho = |z|\) è il modulo di \( z\), ossia, la lunghezza del vettore applicato nell’origine, con estremo nel punto corrispondente sul piano complesso a \( z\). \( \theta\) è detto
argomento o anomalia e rappresenta l’angolo tra l’asse reale e la retta individuata dal vettore \(Oz\). Quando un numero complesso è espresso in questo modo, si dice che è espresso in forma trigonometrica o polare.
La forma polare è adatta a semplificare il prodotto ed il quoziente di numeri complessi. Se proviamo a moltiplicare due numeri \( z_1 = \rho_1( cos\theta_1 + \color{#008080}{i} sin\theta_1 )\)
e \( z_2 = \rho_2( cos\theta_2 + \color{#008080}{i} sin\theta_2 )\) abbiamo:
$$ z_1z_2 = \rho_1( cos\theta_1 + \color{#008080}{i} sin\theta_1 )
\rho_2( cos\theta_2 + \color{#008080}{i} sin\theta_2 ) = $$
$$ \rho_1\rho_2\Bigl( cos(\theta1+\theta_2) + \color{#008080}{i} sin(\theta_1 +\theta_2)\Bigr) $$
Che esprime il fatto che il prodotto tra numeri complessi si ottiene moltiplicando i moduli e sommando gli argomenti (stiro-rotazione complessa). Moltiplicando
un numero complesso per se stesso più volte, si perviene alla cosiddetta
formula di De Moivre per la potenza n-esima:
$$ z^n = \Bigl( \rho(cos\theta + \color{#008080}{i}sin\theta) \Bigr)^n
= \rho^n(cos(n\theta)+ \color{#008080}{i}sin(n\theta)) $$
Che riveste un ruolo fondamentale in molte applicazioni all’algebra ed alla teoria dei numeri.
$$ \diamond $$
La formula di Eulero
Ritornando alla rappresentazione di un numero complesso nella forma trigonometrica, osserviamo, come sia possibile mettere in relazione
l’esponenziale con quanto visto finora.
La forma esponenziale, nasce da una delle più belle relazioni della matematica scoperte
dal grande Eulero nei suoi studi in campo complesso.
E’ possibile dimostrare mediante gli sviluppi di Taylor una netta uguaglianza asintotica che porta alla
formula seguente:
$$ e^{i\theta} = cos(\theta)+isen(\theta)$$
Più comunemente nota come identità di Eulero. Se poniamo \(\theta = \pi\) otteniamo una versione ridotta che costituisce forse la più bella equazione della matematica.
$$ {\large e^{i\pi}+1 = 0} $$
Il motivo è evidente, in quanto in essa, come potete osservare, compaiono le costanti fondamentali \(Il numero di Nepero \( e\)\), \(Pi-greco \( \pi\)\), l’\( 1\), lo \( 0 \) e dulcis in fundo (l’unità immaginaria \( i\)). Io direi che si tratta di magia!
Avendo introdotto la forma esponenziale di un numero complesso,
le operazioni di prodotto, quoziente e potenza, si svolgono banalmente,
operando con le proprietà delle potenze, infatti considerando due numeri complessi
\( z = |z|e^{i\theta_z}\) e \( w = |w|e^{i\theta_w}\) abbiamo che:
$$ zw = \Bigl( z = |z|e^{i\theta_z} \Bigr)
\Bigl( w = |w|e^{i\theta_w} \Bigr) = |z||w|e^{i\theta_z+\theta_w} $$
$$ {z \over w} = {\Bigl( z = |z|e^{i\theta_z} \Bigr) \over \Bigl( w = |w|e^{i\theta_w} \Bigr)}
= {|z| \over |w|}e^{i\theta_z-\theta_w} $$
Provando ad estendere l’operazione di elevamento a potenza frazionaria, si entra nel mondo delle radici complesse che meritano, per la loro straordinaria geometria, un paragrafo a se…
$$ \diamond $$
Radici complesse
Una radice è un numero che rappresenta “quante volte devo moltiplicare per se stesso un altro numero, per ottenerne un terzo”. Ad esempio la radice cubica di \\( 8\) è \(3\). Questo significa che per ottenere \( 8\) devo moltiplicare il \(2\) se stesso \( 3\) volte. Così: \( 2\cdot 2\cdot 2 = 8\). Il discorso è del tutto banale, se restiamo in ambito reale. Come possiamo estendere il tutto in campo complesso??
Quel che si fa, è sostanzialmente procedere in maniera del tutto simile al caso reale.
Si definisce radice \( n\)-esima del numero complesso \( z\) la potenza \( n\)-frazionaria di \( z\)
e si indica nel modo seguente: $${ \large \sqrt[n]{z} = \sqrt[n]{|z|e^{i\theta}} =
{1 \over \sqrt{|z|}}e^{i{1\over n}} } $$
E qui entra in scena il concetto di funzione multivoca. Una funzione multivoca, è una funzione a “più valori”, nel senso che non è proprio una funzione tradizionale, ma bensì un oggetto più sofisticato che può far corrispondere ad un singolo valore in “input” molti più valori in “output”. Infatti, il motivo di questa estensione, nasce dal fatto che l’argomento di un numero complesso, può essere sommato o sottratto per multipli interi di \( 2\pi\), senza che il numero complesso di partenza cambi. Questa sorta di “invarianza per angolo giro” porta a tutta una serie di fatti singolari e particolari dei numeri complessi, come quello, per l’appunto, di funzione multivoca, che sfocia poi, nella teoria delle cosidette superfici di Riemann.
Ritornando all’invarianza per angolo giro, possiamo scrivere la seguente uguaglianza:
$$ |z|e^{i\theta} = |z|e^{i(\theta+2k\pi)}$$
Che, come già detto, esprime il fatto che un numero complesso non cambia per multipli interi dell’angolo giro. Di conseguenza, elevando alla ( {1 \over n})
otteniamo la formula per la radice (n)-esima complessa:
$$ {\large \sqrt[n]{z} = z^{1\over n} = \Bigl( |z|e^{i(\theta + 2k\pi)} \Bigr)^{1\over n} =
|z|^{1\over n}e^{i{\theta+2k\pi \over n}} } = $$
$$ = { |z|^{1\over z}e^{i\left({\theta \over n} + {2k\pi\over n}\right)} =
\sqrt[n]{|z|}e^{i\left({\theta \over n} + {2k\pi\over n}\right)} } $$
Si dimostra, che il numero di radici di un polinomio di grado \( n\) è pari ad \( n\), come espresso nel teorema fondamentale dell’algebra. Provando a calcolare un paio di esempi di radici complesse si osserva come le configurazioni delle radici nel piano complesso occupano le posizioni dei vertici di poligoni regolari, cosicché le radici \(n\)-esime sono corrispondono ad \( n\) vertici di un poligono regolare.
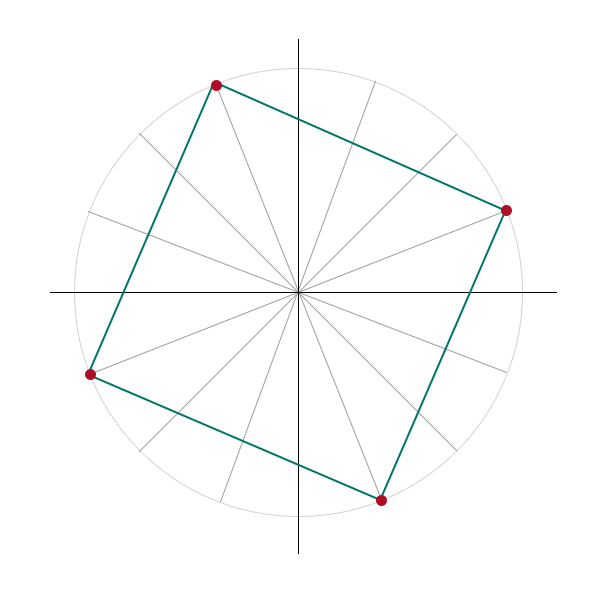
$$ e^{i({\pi \over 2}+2k\pi){1 \over 4}}, \hspace{5mm} k=0, 1, 2, 3 $$
$$\downarrow $$
$$e^{i({\pi \over 8})} \hspace{5mm} e^{i({5\pi \over 8})} \hspace{5mm} e^{i({9\pi \over 8})}
\hspace{5mm} e^{i ({13\pi \over 8})} $$
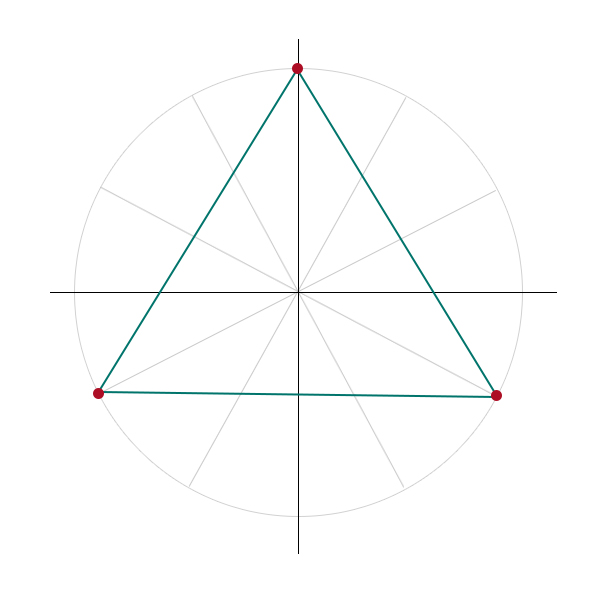
$$ e^{-i({\pi \over 2}+2k\pi){1 \over 3}}, \hspace{5mm} k=0, 1, 2 $$
$$\downarrow $$
$$e^{-i({\pi \over 6})} \hspace{5mm} e^{i({\pi \over 2})} \hspace{5mm} e^{i({7\pi \over 6})} $$

$$ \sqrt[5]{2}e^{i({\pi \over 2}+2k\pi){1 \over 5}}, \hspace{5mm} k=0, 1, 2, 3, 4 $$
$$\downarrow $$
$$\sqrt[5]{2}e^{i({\pi \over 10})} \hspace{5mm} \sqrt[5]{2}e^{i({\pi \over 2})}
\hspace{5mm} \sqrt[5]{2}e^{i({9\pi \over 10})} \hspace{5mm} \ \sqrt[5]{2}e^{i({13\pi \over 10})}
\hspace{5mm} \sqrt[5]{2}e^{i({17\pi \over 10})}$$
$$ {\Large \diamond }$$
\( \langle\langle \)
Per ora concludiamo qui il nostro viaggio… a breve vi fornirò altro materiale. A presto! \( \rangle\rangle \)